Biểu thức mệnh đề là hằng đúng (valid) là một khái niệm quan trọng trong logic toán và khoa học máy tính. Nó chỉ một biểu thức mệnh đề luôn cho giá trị đúng, bất kể giá trị chân lý của các mệnh đề thành phần. Hiểu rõ về tính valid giúp chúng ta xây dựng các lập luận logic chặt chẽ và thiết kế các hệ thống máy tính hoạt động chính xác.
Định Nghĩa Biểu Thức Mệnh Đề Là Hằng Đúng (Valid)
Một biểu thức mệnh đề được gọi là hằng đúng (valid) hay tautology nếu nó luôn luôn đúng, bất kể giá trị chân lý của các mệnh đề con bên trong nó. Nói cách khác, một biểu thức valid luôn trả về giá trị “đúng” trong bảng chân lý của nó, dù các biến mệnh đề được gán giá trị đúng hay sai. Tính valid đảm bảo tính đúng đắn của một biểu thức trong mọi trường hợp.
Phân Biệt Giữa Valid, Satisfiable và Unsatisfiable
Trong logic mệnh đề, chúng ta có ba khái niệm quan trọng cần phân biệt: valid (hằng đúng), satisfiable (có thể thỏa mãn) và unsatisfiable (không thể thỏa mãn).
- Valid (Hằng đúng): Như đã đề cập, biểu thức luôn đúng trong mọi trường hợp.
- Satisfiable (Có thể thỏa mãn): Tồn tại ít nhất một trường hợp mà biểu thức cho giá trị đúng.
- Unsatisfiable (Không thể thỏa mãn): Biểu thức luôn sai trong mọi trường hợp.
Một biểu thức valid cũng đồng thời là satisfiable, nhưng một biểu thức satisfiable chưa chắc đã là valid. Biểu thức unsatisfiable thì không thể là valid.
Ứng Dụng Của Biểu Thức Mệnh Đề Là Hằng Đúng (Valid)
Tính valid của biểu thức mệnh đề có nhiều ứng dụng quan trọng trong thực tế, đặc biệt là trong khoa học máy tính và logic toán.
- Kiểm chứng tính đúng đắn của lập luận: Trong lập luận logic, nếu tiền đề là đúng và biểu thức mệnh đề biểu diễn lập luận là valid, thì kết luận chắc chắn cũng đúng.
- Tối ưu hóa mạch logic: Trong thiết kế mạch điện tử, việc đơn giản hóa các biểu thức logic thành dạng valid giúp giảm thiểu số lượng cổng logic cần thiết, từ đó tiết kiệm chi phí và năng lượng.
- Phát triển hệ thống chứng minh tự động: Các hệ thống chứng minh tự động sử dụng tính valid để kiểm tra tính đúng đắn của các bước chứng minh.
Ví Dụ Về Biểu Thức Mệnh Đề Là Hằng Đúng
Một ví dụ đơn giản về biểu thức mệnh đề hằng đúng là p v ¬p (p hoặc không p). Bất kể p là đúng hay sai, biểu thức này luôn đúng.
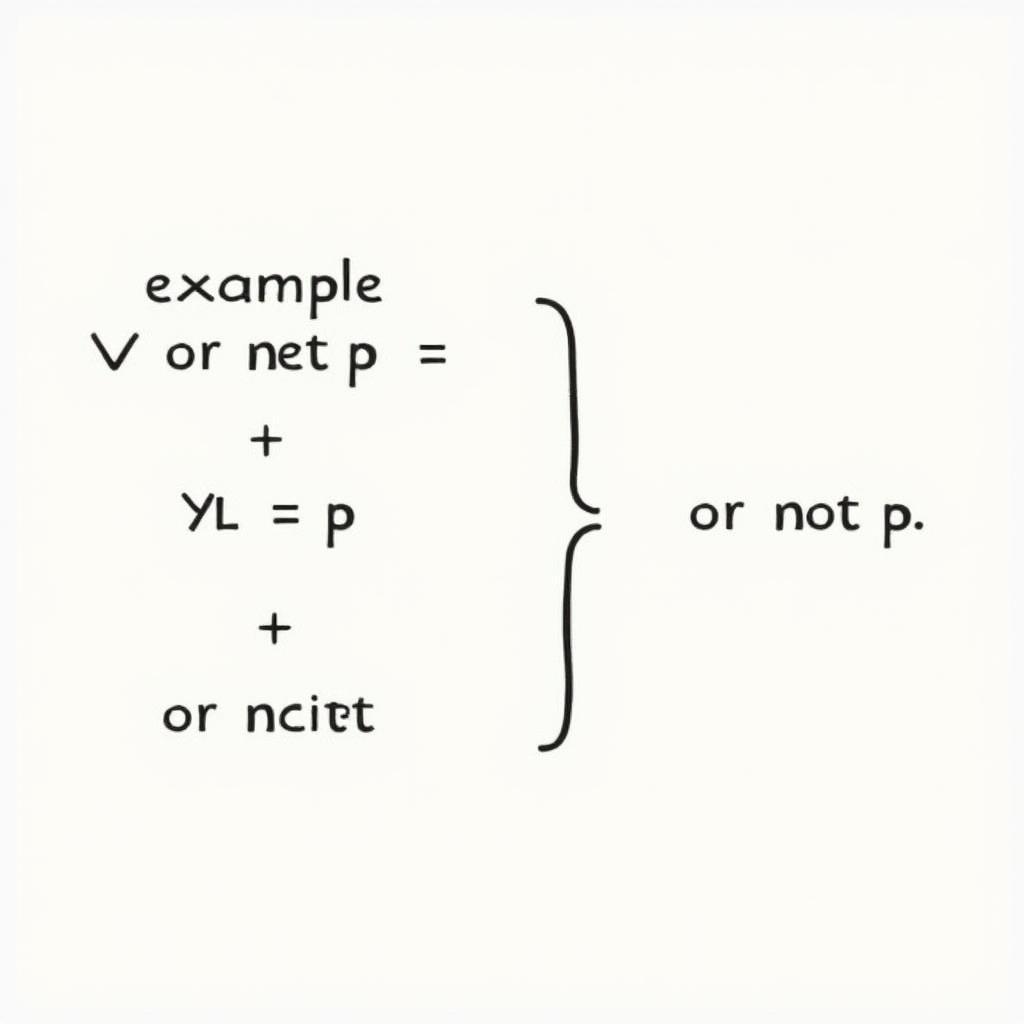Ví dụ minh họa về biểu thức mệnh đề hằng đúng
Kết luận
Biểu thức mệnh đề là hằng đúng (valid) là một khái niệm quan trọng trong logic, đảm bảo tính đúng đắn của biểu thức trong mọi trường hợp. Hiểu rõ về valid, satisfiable và unsatisfiable giúp chúng ta xây dựng lập luận logic chặt chẽ và ứng dụng vào nhiều lĩnh vực khác nhau.
FAQ
- Làm thế nào để kiểm tra một biểu thức mệnh đề có phải là hằng đúng hay không?
- Sự khác biệt giữa valid và satisfiable là gì?
- Ứng dụng của biểu thức mệnh đề hằng đúng trong lập trình là gì?
- Có công cụ nào hỗ trợ kiểm tra tính valid của biểu thức mệnh đề không?
- Tính valid có liên quan gì đến logic mờ không?
- Tại sao việc hiểu về biểu thức mệnh đề hằng đúng lại quan trọng?
- Làm thế nào để đơn giản hóa một biểu thức mệnh đề phức tạp thành dạng valid?
Mô tả các tình huống thường gặp câu hỏi.
Người dùng thường thắc mắc về cách xác định tính valid của một biểu thức, phân biệt nó với các khái niệm khác như satisfiable và unsatisfiable, cũng như ứng dụng của nó trong thực tế.
Gợi ý các câu hỏi khác, bài viết khác có trong web.
Bạn có thể tìm hiểu thêm về các khái niệm liên quan như bảng chân lý, logic mệnh đề, và các phương pháp chứng minh định lý.
